Avicenna Journal of Pharmaceutical Research. :91-97.
doi: 10.34172/ajpr.1074
Original Article
Dynamic In Silico Model of Type 2 Diabetes Treated With Metformin Combined With Exercise: A Sobol Sensitivity Analysis
Darshna M. Joshi 1, * 
Author information:
1Department of Instrumentation and Control, Government Polytechnic Ahmedabad, Ahmedabad 380015, Gujarat, India
Abstract
Background: The widespread adoption of a sedentary lifestyle characterized by the consumption of a high-energy diet combined with a lack of physical activity has resulted in a rise in the prevalence of metabolic disorders like type 2 diabetes (T2D) globally. The data published by the International Diabetes Federation (IDF) every year catches the attention of the world. Insulin resistance results in the dysregulation of the control mechanism that leads to T2D. In addition to metformin as a globally prescribed drug, physical exercise is recommended for the treatment of T2D as an alternative therapy. In today’s systems biology era, sensitivity analysis plays a major role in providing deeper insights into the metabolic insulin signalling pathways (ISPs).
Methods: Here, the complex in silico dynamic model of the effect of alternative therapies on T2D was examined. In order to obtain more quantitative information about the signal transduction network of the ISPs and their interaction, a global sensitivity analysis of the in silico model was carried out using the MATLAB tool.
Results: This study sheds light on the effect of parameter perturbation on the ISP via GLUT4 translocation in T2D patients performing physical exercise and using metformin. It also allows for the selection of a variety of parameters for in vivo or in vitro studies in the future on the basis of the impact of parameter variations on each component of the pathway.
Conclusion: The Sobol index for each condition was noted after introducing perturbations in the most sensitive parameters. These results can provide experimental guidance on how the variations in model inputs have affected the model outputs.
Keywords: Insulin signalling, Global sensitivity analysis, Diabetes, In silico, Sobol index, MATLAB
Copyright and License Information
© 2022 The Author(s); Published by Hamadan University of Medical Sciences.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (
https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Please cite this article as follows: Joshi DM. Dynamic in Silico model of type 2 diabetes treated with metformin combined with exercise: a sobol sensitivity analysis. Avicenna J Pharm Res. 2022; 3(2):91-97. doi:10.34172/ajpr.1074
Introduction
According to recent estimates, diabetes is one of the most common chronic metabolic diseases worldwide, as per the International Diabetes Federation (IDF), and it affects approximately 463 million adults, with a prediction to reach 700 million by 2045 (1). The inability of our body to react to the availability of sufficient insulin causes failure in signaling components, which results in the development of insulin resistance (2–5). In systems biology, modeling the complex behavior of signal transduction pathways is an interesting area of research. Experiments to classify the molecular components and interactions in a system of interest are supplemented with mathematical models. Control theory and mathematical modeling are increasingly being used to address complex biological questions concerning the aetiology of diabetes, as they are uniquely suited to gaining system-wide insights (6-9). It is debatable if type 2 diabetes (T2D) can be fully cured. However, for T2D patients, the most commonly prescribed therapies include a healthy lifestyle, decent food, exercise, and allopathic drugs such as metformin (10-23). The importance of exercise in the management of T2D is widely acknowledged. In order to detect the initiation and metabolism of a T2D patient, an in silico analysis of the effects of physical activity on the GLUT4 translocation is important. There are many statistical analyses available, but there are very few mathematical models and in silico studies in this area. Alternative therapies such as exercise and acupuncture are explored as advanced and common remedies for T2D in response to unsatisfactory drug use in a recent survey (24-43). The mathematical model developed by Sedaghat et al specifically represents the complexities of metabolic insulin signalling pathways (ISPs) and simulates the dynamics of various components involved in signal transduction mediating GLUT4 translocation in skeletal muscle (44). Joshi et al created an in silico dynamic model that quantifies the impact of exercise and metformin on GLUT4 translocation by extending the model developed by Sedaghat et al. The signaling pathways that show the effect of exercise and metformin were incorporated into the in silicomodel, and the results were satisfactory (21).
In the present work, the dynamic in silicomodel developed by Joshi et al (21) was utilized, and perturbations were introduced to analyze the impact on GLUT4 concentration via sensitivity analysis. The sensitivity analysis method is used to assess the relationships between input parameters and model outcomes. Sensitivity analysis helps one to investigate the effects of changing system parameters from their normal state and to define the parameters that influence system behavior. The information gathered can be useful in gaining a better understanding of the context and proposing hypotheses regarding key processes in a system. Additionally, a background can be obtained for speculating about how we could interfere with the system to generate specific behaviors. Parameter sensitivity analysis is a method for determining how different parameters enhance the outcome. The output is said to be responsive to a parameter if it has a significant impact on the output in comparison to the other parameters. The most significant parameters in a model can be identified using sensitivity analysis. Many of the parameters in mathematical models of biological and other complex systems are not or cannot be precisely defined. Sensitivity analysis refers to a collection of techniques for evaluating the effect of parameter uncertainty on a model. Numerous researchers have used a variety of techniques to conduct sensitivity analysis on the model developed by Sedaghat et al (44). Drugs may be able to target key parameters to improve disorders.
Kwei et al carried out the sensitivity analysis on the Sedaghat model of ISPs with feedback to reduce the parameter estimation error. It was done by optimizing the input perturbation and state measurement choices. The results revealed a range of sensitive parameters appropriate for drug targeting (45). Based on the models developed by Sedaghat et al, Liu et al used dynamic sensitivity and control analyses to investigate the GLUT4 metabolic ISPs. They measured the time-dependent sensitivities of membrane GLUT4 concentrations in relation to all reaction parameters. The findings were in line with experimental findings and estimates of drug targets in the literature (46). Further, local parametric sensitivity analysis was carried out by Gray on the ISPs as per the Sedaghat model. The parametric sensitivity analysis disclosed a number of key aspects of the model. Across the spectrum of insulin concentrations, the sensitivity of several parameters changed considerably. The results were used to identify the major regulatory positions in the signaling network as well as network weaknesses. The parameter sensitivity analysis also identified areas where the model could be improved. Additionally, since experimental measurements in biological systems can be scarce, it is critical to create an experimental design that can extract as much information about model parameter values as possible from small and noisy data sets. Since the Sedaghat model lacks experimental validation, Kwei et al used parameter sensitivity analysis to construct experimental designs that are efficient for model identification, given constraints on measurement error and cost (45). Charzyńska et al performed a sensitivity analysis on the membrane receptor system using a mathematical model developed by Shankaran et al. The use of a deterministic system was justified in any case because of the conclusions drawn from the findings. Furthermore, some of the parameters were found to have a minor effect on the results of the system (47,48). As can be seen from the literature, different methods have been used to conduct sensitivity analysis on the ISPs. However, sensitivity analysis of the in silicomodel that takes into account the impact of exercise and metformin on GLUT4 translocation in ISPs in T2D patients is still lacking. The present research work is the first attempt to perform global parametric sensitivity analysis using the Sobol method on the dynamic in silico model developed by Joshi et al (21), which quantifies the effect of exercise and metformin on GLUT4 translocation. Both in vivo and in vitro experiments are expensive and time-consuming. As a result, this analysis of the in silico model will aid in the cost-effective execution of a number of experiments without the use of actual cells. The findings of the global sensitivity analysis of the in silico model of the impact of exercise and metformin on ISPs could be used as a refinement tool in the discovery of combinatorial anti-diabetic drugs.
Exercise and Metformin Interaction With ISPs in T2D: Dynamic In Silico Model
The dynamic in silico model has already been published recently. To establish a connection for the reader, here is a brief explanation. For a detailed description, one may refer to the paper by Joshi et al (21). The signaling pathways are made up of a complex system with several inputs, outputs, and interactions. While a complete understanding of this complex structure is still a work in progress, the basic mechanisms that govern GLUT4 translocation are well understood. AMPK activation mechanisms are the main drivers of GLUT4 translocation. The effects of insulin, metformin, and physical activity on GLUT4 translocation are depicted in Figure 1 and can be simulated using Cell Designer software (49,50). The ISP is composed primarily of insulin, which binds to the insulin receptor and induces autophosphorylation and activation. Insulin receptor substrate-1 (IRS1) is further phosphorylated as a result of this activation, forming a complex with phosphatidylinositol-3-kinase (PI3K). Phosphatidylinositol triphosphate (PIP3) is generated by the IRS1-PI3K complex, which then interacts allosterically with phosphoinositide-dependent kinase 1 (PDK1). Protein kinases AKT and PKC are phosphorylated by the PIP3-PDK1 complex, which then cause glucose transporter (GLUT4) translocation to the cell membrane via an unknown mechanism to uptake glucose. A few other proteins influence the activity of this pathway (44,51). Another pathway is the activation of AMP-activated protein kinase (AMPK) by exercise and metformin, which then catalyzes PKC phosphorylation and increases GLUT4 translocation to the plasma membrane (52-54). For the dynamic model, the value of PTP was changed from 1 to 1.5 to simulate T2D. Moreover, the exercise intensity was simulated on the basis of changes in cellular energy, which is represented by parameter kstim (a parameter to represent exercise intensity) in the model. The values and parameters can be referred to in detail in published papers (21,54).
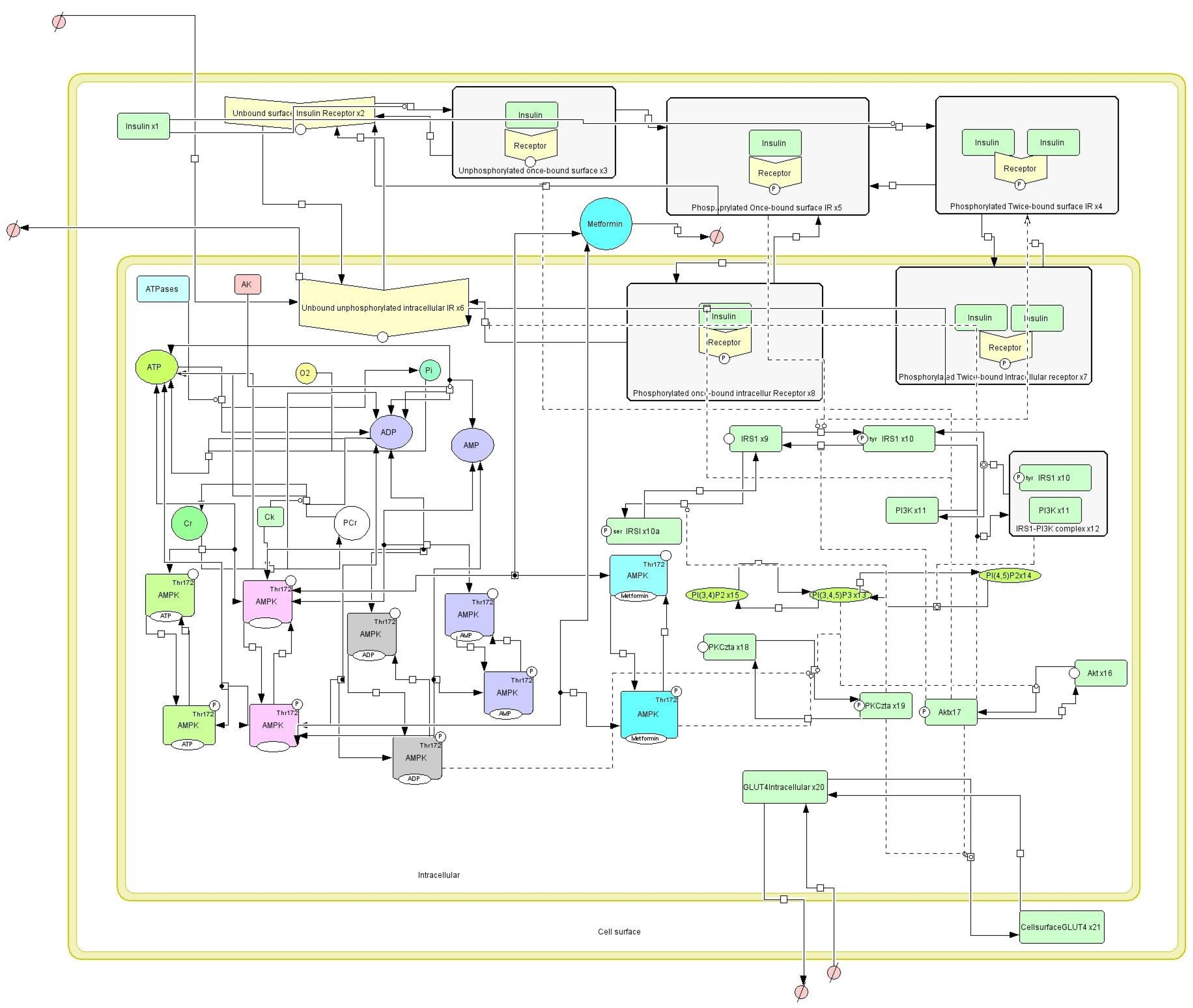
Figure 1.
Dynamic In SilicoModel of T2D (Exercise Intensity of 1 and Metformin Dose of 500 mg) (21).
.
Dynamic In SilicoModel of T2D (Exercise Intensity of 1 and Metformin Dose of 500 mg) (21).
Considering that the impact of exercise and metformin on the GLUT4 translocation was established quantitatively, a Sobol-based sensitivity analysis was carried out to analyze the impact of individual parameters and their interactions on the GLUT4 translocation in a person with T2D who performed exercise and used metformin. This is the first time such an analysis has been performed on a dynamic in silico model of T2D with a metformin dose of 500 mg and an exercise intensity of kstim = 1.
Sobol Sensitivity Analysis: Methodology
Global sensitivity analysis is an effective approach that determines which parameters and their interactions are the most influential in the overall behavior of the model over the entire parameter space. Several global sensitivity analysis methods, such as multiparametric sensitivity analysis and Sobol’s method, are available for the model. Zhang et al conducted a study summarizing the distinct features of each method (55). Among all the methods of global sensitivity analysis summarized, Sobol sensitivity analysis based on variance decomposition is currently one of the most powerful techniques (56-59).
In Sobol-based global sensitivity analysis, the variance of the output of the model is decomposed into fractions that are attributed to various inputs or their interactions. The ultimate aim of a Sobol sensitivity analysis is to figure out the variability that is observed in the performance of the model due to each input parameter or the interaction of various input parameters. The first-order Sobol index measures the effect of individual parameters on output variance. The total order Sobol index measures the effect of individual parameters and their interactions with other parameters on the output variance. Therefore, the entire parameter space is covered. The higher the value of the Sobol index, the more influential the respective model parameter. Although there are no established rules for selecting the significance level, 0.05 is commonly used for performing the analysis. The significance level was used to identify the relative importance of parameters. For the present research work, our recently published dynamic in silicomodel was used (44). Sobol-based global sensitivity analysis was carried out on the in silico dynamic model as shown in Figure 1. MATLAB was used as a tool for global sensitivity analysis to perform Sobol analysis on the dynamic in silicomodel. The steps to perform a Sobol sensitivity analysis were as follows:
-
Import an in silico model from Cell Designer to SimBiology in MATLAB
-
Export the model from SimBiology to a MATLAB workspace
-
Launch the global sensitivity analysis
-
Select the Sobol sensitivity analysis parameters
-
Select the total number of samples
-
Provide ranges for the selected parameters
-
Select the output parameter (GLUT4)
-
Perform computation
-
Examine the first and total order Sobol indices
The initial values of each parameter are taken from the literature (44) and our recently published paper (21). Considering that we had a greater number of parameters for the simulated dynamic in silico model, we carried out global sensitivity analysis on all the input parameters at first with a given range of ± 10% perturbation, as shown in Figure 2. It is important to note that the details of all the parameters can be obtained through the model developed by Sedaghat and the model developed by Joshi et al (21).
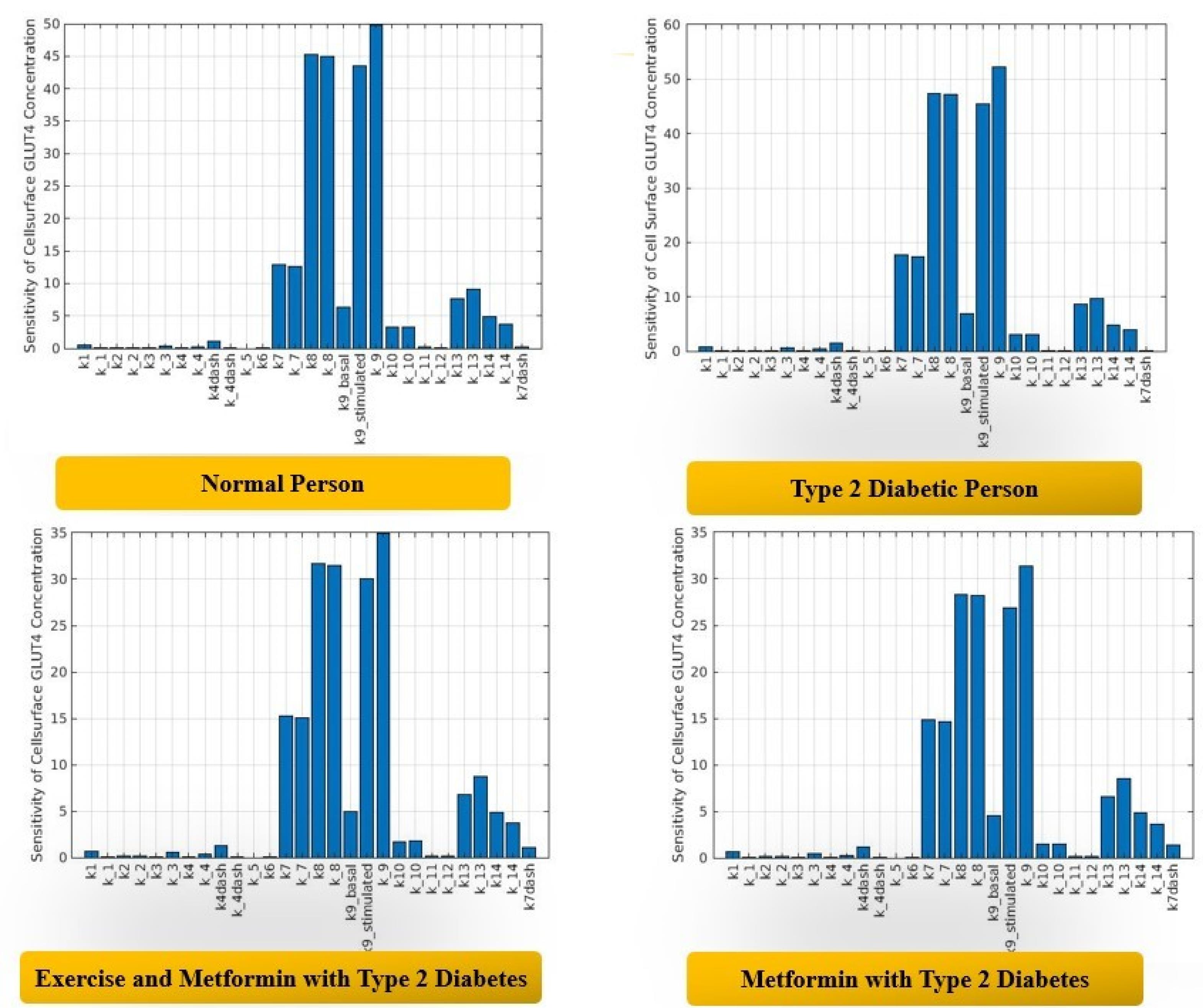
Figure 2.
Global Sensitivity Analysis of Insulin Signaling Pathways.
.
Global Sensitivity Analysis of Insulin Signaling Pathways.
The surface GLUT4 concentration was chosen as the output parameter. After analyzing the Sobol indices of all the parameters, those having a significance level of more than 0.05 were chosen for the second round of the Sobol sensitivity analysis with a varied range of perturbation for each parameter. The results obtained for each condition of the dynamic in silico model are discussed in the following section.
Results and Discussion
The application of a dynamic in silicomodel is the ultimate goal of the sensitivity analysis. Here, the Sobol-based sensitivity analysis was carried out to investigate the following aspects:
-
Impact on GLUT4 under normal conditions
-
Impact on GLUT4 under type 2 diabetic conditions
-
Impact on GLUT4 when an individual with T2D uses metformin
-
Impact on GLUT4 when a person with T2D takes 500 mg of metformin and engages in physical activity at an intensity of kstim = 1
First, Sobol sensitivity analysis was carried out for all the parameters under normal conditions within the range of ± 10%. For each parameter, we examined the first and total order Sobol indices. Those parameters with a Sobol index value greater than 0.05 were considered significant and were chosen for further Sobol sensitivity analysis in all of the cases mentioned above. The range of the selected significant parameters was determined by performing a multiparametric global sensitivity analysis on all of the parameters under normal conditions with the classifier (max (GLUT4 concentration) > 30%). We chose the range for each parameter that showed a larger impact on the GLUT4 concentration, and then we performed the Sobol sensitivity analysis for all the cases. The parameters that were chosen for the final Sobol sensitivity analysis with a significance value greater than 0.05 included k7, k_7, k8, k_8, k9_stimulated, k_9, k13, and k_13.
The variation in the Sobol indices was clearly observed in Figure 3 when we compared the values for various conditions. The values of the first and total order Sobol indices are noted in Table 1 under all the conditions.
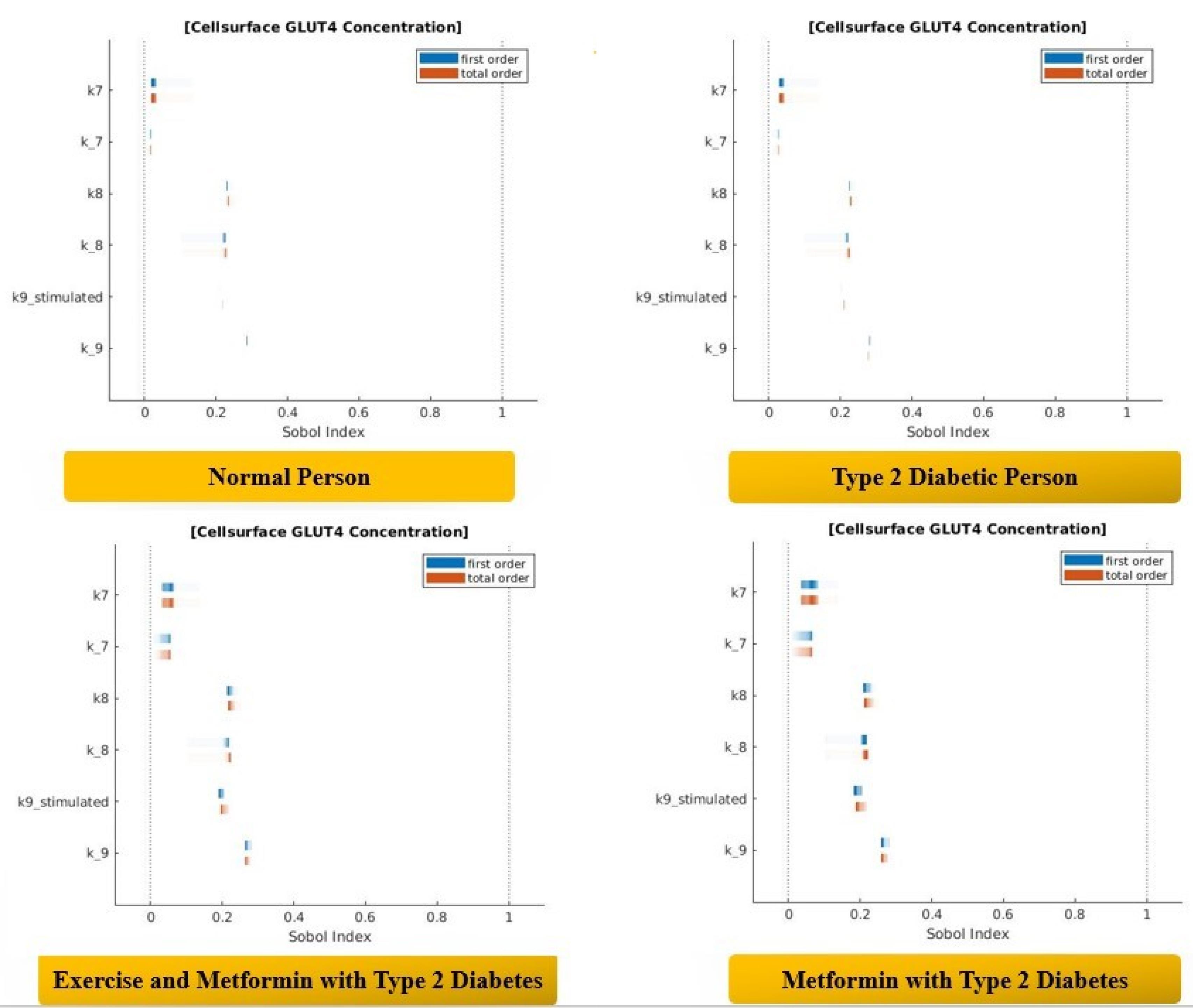
Figure 3.
Sobol Analysis of Insulin Signaling Pathways.
.
Sobol Analysis of Insulin Signaling Pathways.
Table 1.
Sobol Indices
|
Parameters
|
Normal
|
T2D
|
Metformin (500 mg)
|
Metformin (500 mg)+exercise
(kstim=1)
|
|
First Order Sobol Index
|
Total Order Sobol Index
|
First Order Sobol Index
|
Total Order Sobol Index
|
First Order Sobol Index
|
Total Order Sobol Index
|
First Order Sobol Index
|
Total Order Sobol Index
|
| k7 (rate constant for insulin receptor substrate phosphorylation) |
0.12 |
0.13 |
0.13 |
0.13 |
0.11 |
0.12 |
0.12 |
0.13 |
| k_7 (rate constant for insulin receptor substrate dephosphorylation) |
0.01 |
0.01 |
0.02 |
0.02 |
0.03 |
0.03 |
0.02 |
0.03 |
| k8 (rate constant for insulin receptor substrate 1 complex formation) |
0.03 |
0.03 |
0.03 |
0.02 |
0.15 |
0.15 |
0.02 |
0.02 |
| k_8 (rate constant for insulin receptor substrate 1 complex reversed) |
0.23 |
0.23 |
0.22 |
0.22 |
0.17 |
0.19 |
0.22 |
0.22 |
| k9_stimulated (rate constant of PIP2 to PIP3 formation) |
0.27 |
0.28 |
0.26 |
0.26 |
0.23 |
0.22 |
0.25 |
0.26 |
| k_9 (rate constant of PIP3 to PIP2 formation) |
0.43 |
0.42 |
0.42 |
0.42 |
0.35 |
0.35 |
0.41 |
0.41 |
| k13 (rate constant for translocation of GLUT4 to the cell surface under basal condition) |
0.09 |
0.09 |
0.10 |
0.10 |
0.06 |
0.06 |
0.09 |
0.09 |
| k_13 (rate constant for translocation of GLUT4) |
0.24 |
0.24 |
0.22 |
0.22 |
0.22 |
0.22 |
0.23 |
0.23 |
It was observed that the Sobol index value for a certain parameter was higher when a person was type 2 diabetic in comparison to those under normal conditions. This shows that the impact of parameters on the variance in GLUT4 concentration is more pronounced when a person becomes type 2 diabetic. Surprisingly, after obtaining the Sobol indices for the cases with metformin alone and with metformin and exercise, a significant difference in GLUT4 concentration was observed. This shows that when a type 2 diabetic person uses metformin, the impact of parameters on the GLUT4 concentration changes in comparison to that under normal conditions. Additionally, when exercise is combined with metformin, a significant variation in the GLUT4 concentration is observed.
For all the cases, it was clearly observed that when perturbations are introduced to the sensitive parameters, the impact on the output is different in every condition. Therefore, this approach can be utilized to predict the effect of parameter variations on the T2D targets used in drug development and testing, which can bring about a revolution in the pharmaceutical industry.
Conclusion
Sensitivity analysis plays a major role in understanding the impact of variations in the output parameters caused by input perturbations. The Sobol sensitivity analysis concept was used in this study to understand the impact of alternative therapies such as physical exercise and metformin as an allopathic drug on the surface GLUT4 concentration for variations in the globally sensitive input parameters using MATLAB and Cell Designer. Variations in Sobol indices clearly demonstrated different levels of impact on output under various input conditions in both normal and T2D states. In the future, these results could be utilized in the pharmaceutical industry to identify the global target for metabolic disorders like T2D and perform in vivo and in vitro analyses.
Competing Interests
The authors declare that they have no conflict of interests.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
References
- International Diabetes Federation (IDF). IDF Diabetes Atlas. 9th ed. Brussels: IDF; 2019.
- IDF. The IDF Consensus Worldwide Definition of the Metabolic Syndrome. Available from: https://sites.pitt.edu/~super1/Metabolic/IDF1.pdf.
- Taylor R. Insulin resistance and type 2 diabetes. Diabetes 2012; 61(4):778-9. doi: 10.2337/db12-0073 [Crossref] [ Google Scholar]
- Czech MP. Insulin action and resistance in obesity and type 2 diabetes. Nat Med 2017; 23(7):804-14. doi: 10.1038/nm.4350 [Crossref] [ Google Scholar]
- Pessin JE, Saltiel AR. Signaling pathways in insulin action: molecular targets of insulin resistance. J Clin Invest 2000; 106(2):165-9. doi: 10.1172/jci10582 [Crossref] [ Google Scholar]
- Baetica A-A, Westbrook A, El-Samad H. Control theoretical concepts for synthetic and systems biology. Curr Opin Syst Biol 2019; 14:50-7. doi: 10.1016/j.coisb.2019.02.010 [Crossref] [ Google Scholar]
- Liu E, Yuan JM. Dynamic sensitivity and control analyses of metabolic insulin signalling pathways. IET Syst Biol 2010; 4(1):64-81. doi: 10.1049/iet-syb.2008.0178 [Crossref] [ Google Scholar]
- Ruoff P, Agafonov O, Tveit DM, Thorsen K, Drengstig T. Homeostatic controllers compensating for growth and perturbations. PLoS One 2019; 14(8):e0207831. doi: 10.1371/journal.pone.0207831 [Crossref] [ Google Scholar]
- Cloutier M, Wellstead P. The control systems structures of energy metabolism. J R Soc Interface 2010; 7(45):651-65. doi: 10.1098/rsif.2009.0371 [Crossref] [ Google Scholar]
- Cao S, Li B, Yi X, Chang B, Zhu B, Lian Z. Effects of exercise on AMPK signaling and downstream components to PI3K in rat with type 2 diabetes. PLoS One 2012; 7(12):e51709. doi: 10.1371/journal.pone.0051709 [Crossref] [ Google Scholar]
- Olokoba AB, Obateru OA, Olokoba LB. Type 2 diabetes mellitus: a review of current trends. Oman Med J 2012; 27(4):269-73. doi: 10.5001/omj.2012.68 [Crossref] [ Google Scholar]
- Koosnadi S, Suhariningsih S, Adikara RTS, Sagiran S, Felix T. Scientific based of acupuncture as alternative treatment of diabetes mellitus. Bul Penelit Sist Kesehat 2010; 13(3):247-56. doi: 10.22435/bpsk.v13i3Jul.2260 [Crossref] [ Google Scholar]
- Chen D, Gong D, Zhai Y. Clinical and experimental studies in treating diabetes mellitus by acupuncture. J Tradit Chin Med 1994; 14(3):163-6. [ Google Scholar]
- Conn VS, Koopman RJ, Ruppar TM, Phillips LJ, Mehr DR, Hafdahl AR. Insulin sensitivity following exercise interventions: systematic review and meta-analysis of outcomes among healthy adults. J Prim Care Community Health 2014; 5(3):211-22. doi: 10.1177/2150131913520328 [Crossref] [ Google Scholar]
- Visen PK, Visen AS, Visen SS, Buttar HS, Singh RB. Management of type 2 diabetes and atherosclerosis with alternative therapies. World Heart J 2015; 7(1):63-82. [ Google Scholar]
- Krook A, Roth RA, Jiang XJ, Zierath JR, Wallberg-Henriksson H. Insulin-stimulated Akt kinase activity is reduced in skeletal muscle from NIDDM subjects. Diabetes 1998; 47(8):1281-6. doi: 10.2337/diab.47.8.1281 [Crossref] [ Google Scholar]
- Balducci S, Sacchetti M, Haxhi J, Orlando G, D’Errico V, Fallucca S. Physical exercise as therapy for type 2 diabetes mellitus. Diabetes Metab Res Rev 2014; 30 Suppl 1:13-23. doi: 10.1002/dmrr.2514 [Crossref] [ Google Scholar]
- Malhotra V, Singh S, Tandon OP, Madhu SV, Prasad A, Sharma SB. Effect of yoga asanas on nerve conduction in type 2 diabetes. Indian J Physiol Pharmacol 2002; 46(3):298-306. [ Google Scholar]
- Derouich M, Boutayeb A. The effect of physical exercise on the dynamics of glucose and insulin. J Biomech 2002; 35(7):911-7. doi: 10.1016/s0021-9290(02)00055-6 [Crossref] [ Google Scholar]
- Hussey SE, McGee SL, Garnham A, Wentworth JM, Jeukendrup AE, Hargreaves M. Exercise training increases adipose tissue GLUT4 expression in patients with type 2 diabetes. Diabetes Obes Metab 2011; 13(10):959-62. doi: 10.1111/j.1463-1326.2011.01426.x [Crossref] [ Google Scholar]
- Joshi DM, Patel J, Bhatt H. In silico study to quantify the effect of exercise on surface GLUT4 translocation in diabetes management. Netw Model Anal Health Inform Bioinform 2021; 10(1):1. doi: 10.1007/s13721-020-00274-3 [Crossref] [ Google Scholar]
- Holloszy JO. Exercise-induced increase in muscle insulin sensitivity. J Appl Physiol (1985) 2005; 99(1):338-43. doi: 10.1152/japplphysiol.00123.2005 [Crossref] [ Google Scholar]
- Amanat S, Ghahri S, Dianatinasab A, Fararouei M, Dianatinasab M. Exercise and type 2 diabetes. Adv Exp Med Biol 2020; 1228:91-105. doi: 10.1007/978-981-15-1792-1_6 [Crossref] [ Google Scholar]
- Ma L, Iglesias PA. Quantifying robustness of biochemical network models. BMC Bioinformatics 2002; 3:38. doi: 10.1186/1471-2105-3-38 [Crossref] [ Google Scholar]
- Eddouks M, Maghrani M. Phlorizin-like effect of Fraxinus excelsior in normal and diabetic rats. J Ethnopharmacol 2004; 94(1):149-54. doi: 10.1016/j.jep.2004.05.005 [Crossref] [ Google Scholar]
- Sung CK, Goldfine ID. Insulin receptor signaling. In: Lee AG, ed. Biomembranes: A Multi-Volume Treatise. Vol 6. JAI; 1997. p. 3-15. 10.1016/s1874-5342(96)80030-4.
- Giri L, Mutalik VK, Venkatesh KV. A steady state analysis indicates that negative feedback regulation of PTP1B by Akt elicits bistability in insulin-stimulated GLUT4 translocation. Theor Biol Med Model 2004; 1:2. doi: 10.1186/1742-4682-1-2 [Crossref] [ Google Scholar]
- Østergård T, Andersen JL, Nyholm B, Lund S, Nair KS, Saltin B. Impact of exercise training on insulin sensitivity, physical fitness, and muscle oxidative capacity in first-degree relatives of type 2 diabetic patients. Am J Physiol Endocrinol Metab 2006; 290(5):E998-1005. doi: 10.1152/ajpendo.00012.2005 [Crossref] [ Google Scholar]
- Malhotra V, Singh S, Tandon OP, Sharma SB. The beneficial effect of yoga in diabetes. Nepal Med Coll J 2005; 7(2):145-7. [ Google Scholar]
- Bay R, Bay F. Combined therapy using acupressure therapy, hypnotherapy, and transcendental meditation versus placebo in type 2 diabetes. J Acupunct Meridian Stud 2011; 4(3):183-6. doi: 10.1016/j.jams.2011.09.006 [Crossref] [ Google Scholar]
- Raveendran AV, Deshpandae A, Joshi SR. Therapeutic role of yoga in type 2 diabetes. Endocrinol Metab (Seoul) 2018; 33(3):307-17. doi: 10.3803/EnM.2018.33.3.307 [Crossref] [ Google Scholar]
- Manyam BV. Diabetes mellitus, Ayurveda, and yoga. J Altern Complement Med 2004; 10(2):223-5. doi: 10.1089/107555304323062185 [Crossref] [ Google Scholar]
- Mann S, Beedie C, Balducci S, Zanuso S, Allgrove J, Bertiato F. Changes in insulin sensitivity in response to different modalities of exercise: a review of the evidence. Diabetes Metab Res Rev 2014; 30(4):257-68. doi: 10.1002/dmrr.2488 [Crossref] [ Google Scholar]
- Innes KE, Selfe TK. Yoga for adults with type 2 diabetes: a systematic review of controlled trials. J Diabetes Res 2016; 2016:6979370. doi: 10.1155/2016/6979370 [Crossref] [ Google Scholar]
- Hooper PL. Hot-tub therapy for type 2 diabetes mellitus. N Engl J Med 1999; 341(12):924-5. doi: 10.1056/nejm199909163411216 [Crossref] [ Google Scholar]
- Hu D, Yuan JM. Time-dependent sensitivity analysis of biological networks: coupled MAPK and PI3K signal transduction pathways. J Phys Chem A 2006; 110(16):5361-70. doi: 10.1021/jp0561975 [Crossref] [ Google Scholar]
- Boucher J, Kleinridders A, Kahn CR. Insulin receptor signaling in normal and insulin-resistant states. Cold Spring Harb Perspect Biol 2014; 6(1):a009191. doi: 10.1101/cshperspect.a009191 [Crossref] [ Google Scholar]
- Kraniou GN, Cameron-Smith D, Hargreaves M. Acute exercise and GLUT4 expression in human skeletal muscle: influence of exercise intensity. J Appl Physiol (1985) 2006; 101(3):934-7. doi: 10.1152/japplphysiol.01489.2005 [Crossref] [ Google Scholar]
- Stumvoll M, Goldstein BJ, van Haeften TW. Type 2 diabetes: principles of pathogenesis and therapy. Lancet 2005; 365(9467):1333-46. doi: 10.1016/s0140-6736(05)61032-x [Crossref] [ Google Scholar]
- Vinod PK, Venkatesh KV. Quantification of signaling networks. J Indian Inst Sci 2008; 88(1):1-26. [ Google Scholar]
- Colmekci C. The Insulin Signalling Pathway in Skeletal Muscle: In Silico and in Vitro [thesis]. Technische Universiteit Eindhoven; 2015.
- Kraniou Y, Cameron-Smith D, Misso M, Collier G, Hargreaves M. Effects of exercise on GLUT-4 and glycogenin gene expression in human skeletal muscle. J Appl Physiol (1985) 2000; 88(2):794-6. doi: 10.1152/jappl.2000.88.2.794 [Crossref] [ Google Scholar]
- Ozougwu JC, Obimba KC, Belonwu CD, Unakalamba CB. The pathogenesis and pathophysiology of type 1 and type 2 diabetes mellitus. J Physiol Pathophysiol 2013; 4(4):46-57. doi: 10.5897/jpap2013.0001 [Crossref] [ Google Scholar]
- Sedaghat AR, Sherman A, Quon MJ. A mathematical model of metabolic insulin signaling pathways. Am J Physiol Endocrinol Metab 2002; 283(5):E1084-101. doi: 10.1152/ajpendo.00571.2001 [Crossref] [ Google Scholar]
- Kwei EC, Sanft KR, Shoemaker JE, Petzold LR, Doyle Iii FJ. Stochastic simulation and systems analysis of insulin-stimulated GLUT4 translocation. In: AIChE Annual Meeting, Conference Proceedings; 2008.
- Zi Z. Sensitivity analysis approaches applied to systems biology models. IET Syst Biol 2011; 5(6):336-346. doi: 10.1049/iet-syb.2011.0015 [Crossref] [ Google Scholar]
- Charzyńska A, Nałęcz A, Rybiński M, Gambin A. Sensitivity analysis of mathematical models of signaling pathways. BioTechnologia 2012; 93(3):291-308. doi: 10.5114/bta.2012.46584 [Crossref] [ Google Scholar]
- Behar M, Barken D, Werner SL, Hoffmann A. The dynamics of signaling as a pharmacological target. Cell 2013; 155(2):448-61. doi: 10.1016/j.cell.2013.09.018 [Crossref] [ Google Scholar]
- Sauro HM, Bergmann FT. Software tools for systems biology. In: Liu ET, Lauffenburger DA, eds. Systems Biomedicine. San Diego: Academic Press; 2010. p. 289-314. 10.1016/b978-0-12-372550-9.00012-2.
- Funahashi A, Matsuoka Y, Jouraku A, Morohashi M, Kikuchi N, Kitano H. CellDesigner 4.3 Startup Guide [Internet]. 2013. Available from: http://www.celldesigner.org/index.html.
- Gray CW, Coster AC. A receptor state space model of the insulin signalling system in glucose transport. Math Med Biol 2015; 32(4):457-73. doi: 10.1093/imammb/dqv003 [Crossref] [ Google Scholar]
- Hardie DG, Hawley SA. AMP-activated protein kinase: the energy charge hypothesis revisited. Bioessays 2001; 23(12):1112-9. doi: 10.1002/bies.10009 [Crossref] [ Google Scholar]
- Messina G, Palmieri F, Monda V, Messina A, Dalia C, Viggiano A. Exercise causes muscle GLUT4 translocation in an insulin-independent manner. Biol Med (Aligarh) 2015; 1:1-4. doi: 10.4172/0974-8369.1000S3007 [Crossref] [ Google Scholar]
- Coccimiglio IF, Clarke DC. ADP is the dominant controller of AMP-activated protein kinase activity dynamics in skeletal muscle during exercise. PLoS Comput Biol 2020; 16(7):e1008079. doi: 10.1371/journal.pcbi.1008079 [Crossref] [ Google Scholar]
- Zhang XY, Trame MN, Lesko LJ, Schmidt S. Sobol sensitivity analysis: a tool to guide the development and evaluation of systems pharmacology models. CPT Pharmacometrics Syst Pharmacol 2015; 4(2):69-79. doi: 10.1002/psp4.6 [Crossref] [ Google Scholar]
- Qian G, Mahdi A. Sensitivity analysis methods in the biomedical sciences. Math Biosci 2020; 323:108306. doi: 10.1016/j.mbs.2020.108306 [Crossref] [ Google Scholar]
- Zi Z, Zheng Y, Rundell AE, Klipp E. SBML-SAT: a systems biology markup language (SBML) based sensitivity analysis tool. BMC Bioinformatics 2008; 9:342. doi: 10.1186/1471-2105-9-342 [Crossref] [ Google Scholar]
- Saltelli A, Tarantola S, Chan KPS. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999; 41(1):39-56. doi: 10.1080/00401706.1999.10485594 [Crossref] [ Google Scholar]
- Yoon J, Deisboeck TS. Investigating differential dynamics of the MAPK signaling cascade using a multi-parametric global sensitivity analysis. PLoS One 2009; 4(2):e4560. doi: 10.1371/journal.pone.0004560 [Crossref] [ Google Scholar]